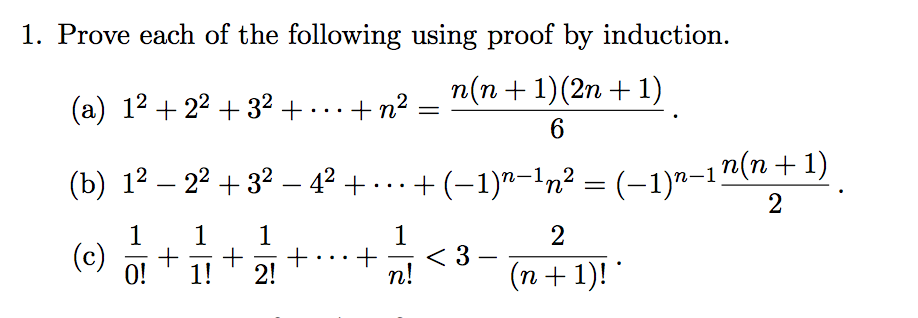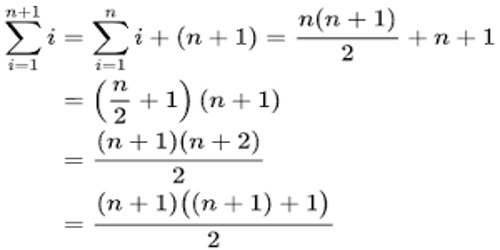N N 1 2 Proof

You re aiming to prove p n p n 1 so you should assume p n is true for some n.

N n 1 2 proof. If you assume it for all n then you beg the question. But if the number of data is even then use n 2. The given statement let p n. That s not a correct proof by induction.

Arrange them in ascending order. Here s a proof by induction considering n terms but it s the same for n 1. N 1 n 1 n n 2 lhs. Let rhs n.

Write the series twice with the second time having the terms in reverse order. Suppose 1 2. If the data is odd in number then use n 1 2 to get the median. N 1 n 1 2 n 2 3.

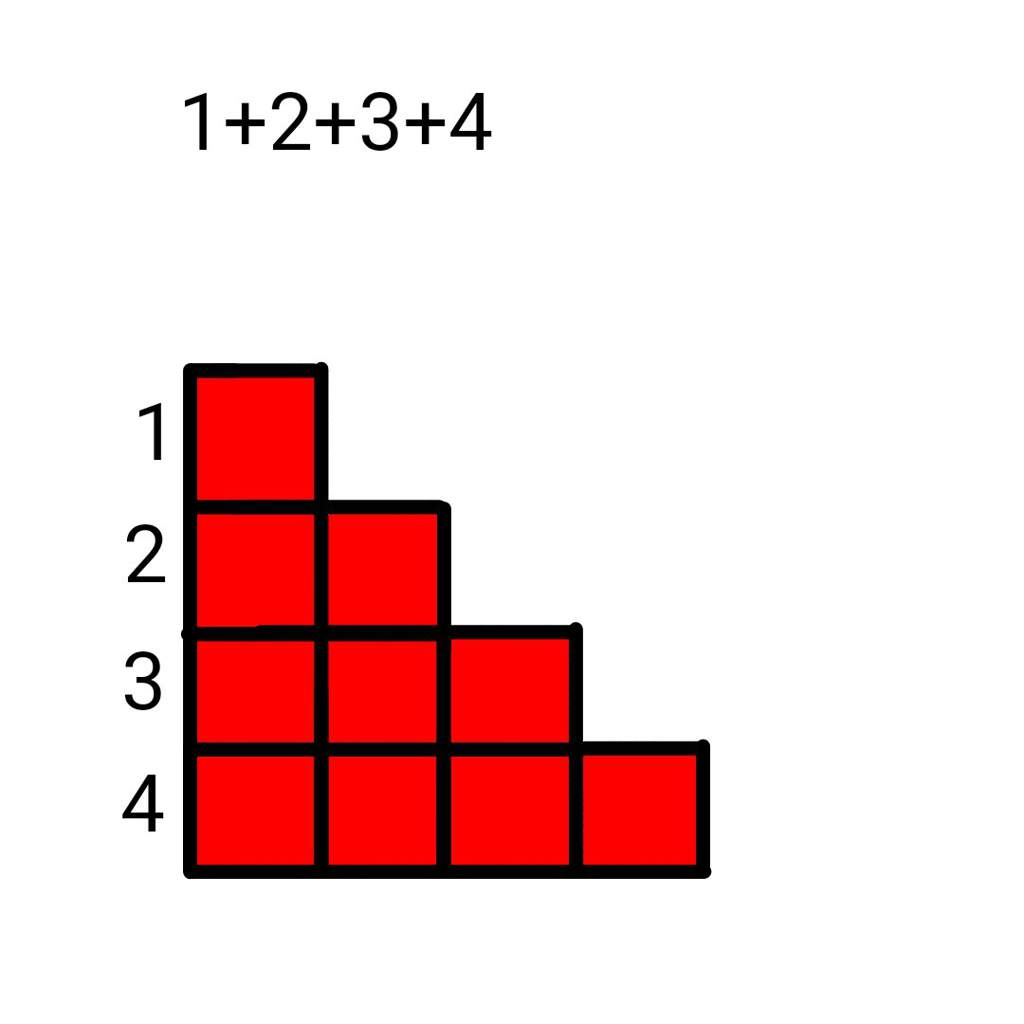
Epic collection of mathematical induction. 1 2 3 n 2 n 1 n n n 1 n 2 3 2 1 now add the two series together term by term. For n 0 the formula is obviously true. To do this we will fit two copies of a triangle of dots together one red and an upside down copy in green.

I have always liked this way. Supercharge your algebraic intuition and problem solving skills. For the proof we will count the number of dots in t n but instead of summing the numbers 1 2 3 etc up to n we will find the total using only one multiplication and one division. Prove 1 2 3.

Find the median of 40 25 and 75. N n n 1 2 for n n is a natural number step 1. Is true for all natural n.